◇数学が苦手で勉強しているけど、思うように成績が上がらない・・・ ◇数学が出来る人はどういう風に問題文を読んで考えているの? ◇問題文を読んだ後、手が止まってしまう・・・ ◇数学って結局才能なの?
このような悩みを抱えている人はたくさんおられるでしょう。
何を隠そう僕もそうでした。ですから気持ちは痛い程わかります。
今日は数学ができる人は数学の問題を解くときどういう思考過程を辿っているのか、このことに関して記事にしたいと思います。
講師歴約7年の僕がこの記事を書いています。
今まで数多くの生徒を指導し、旧帝大や難関大学志望の生徒を志望校へ合格させてきました。
こうした経験を基に本記事を書いています。
数学で一番困るのが問題文を読んでから「どうするんだろう…」と手が止まってしまうことではないでしょうか。
この記事を読むと、問題文から実際に手を動かして問題を解くまでの過程が具体的に理解できるようになると思います。
そして、問題を解く過程が理解できれば、日頃どういうことを意識して勉強するべきか分かると思います。
それでは見ていきましょう!
数学の問題を解くときの思考過程
数学の問題を解くときの思考過程を僕なりに図式化・言語化してみました。
先ずは下の図をご覧ください。
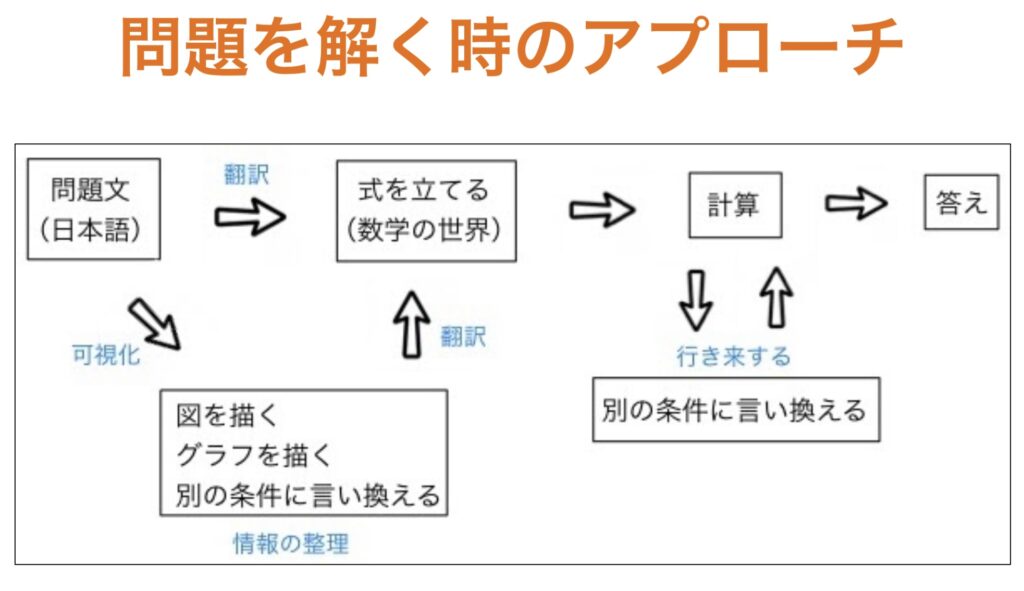
これだけでは意味不明ですよね。
今から順番に説明して行きたいと思います。
『問題文』→『式を立てる』の過程
数学の問題文は、当たり前のことですが、日本語で書かれています。
数式などが問題文に入っていることもありますが、問題文の大部分は日本語で書かれているはずです。
数学として問題を解く為には、何かしらの数式を立てなければなりません。
皆さんも経験があると思いますが、数学の問題はほぼ100%数式を立てて、計算をして…という過程を経て答えまで辿り着いていると思います。
ということは、日本語のままで考えていては(問題文をそのまま読んでいては)数学の問題は解けないのです。
まずはこのことをきちんと認識しましょう。
ではどうすれば良いのか?答えは簡単です。
日本語で記述された問題を『数学の世界の言葉』に言い換えてやれば良いのです。
『数学の世界の言葉』というのは数字・文字・記号またはこれらを用いた式のことです。
僕はこの言い換える作業のことを『翻訳』と読んでいます。
数学が得意な人や出来る人は、この事を意識しているか否かは別にして、問題を解くときに必ず『翻訳』をしていますし、『翻訳』するのが上手です。
具体的な問題を例に出して説明したいと思います。

簡単な問題なので皆さんお分かりだとは思いますが、この問題での翻訳ポイントは『異なる2つの実数解を持つ』という部分です。
「『異なる2つの実数解を持つ』のだから、『判別式D>0』」と考えるはずです。
こういう風に、日本語から数式に言い換えたことがまさに『翻訳』なのです。
例題は簡単な問題なのでそんなことは意識しなくても出来ると思いますが、難しい問題でも考え方は同じです。
まずは問題文を読んで、どのような翻訳ができるかを意識すると突破口が見つかることが多いです。
こうして意識してみると問題文の読み方が変わってくると思います。意識してみて下さい。
『問題文』→『情報の整理』の過程

上の例のような簡単な問題の場合は、すぐに『日本語』→『数式』に『翻訳』することができますが、応用問題などの難しい問題を解こうと思うと、簡単に『翻訳』することはできません。
どうして『翻訳』するのが難しいかというと、翻訳すべき情報が問題文から読み取れず、隠れているからです。
この日本語に表れていない、隠れている情報を引っ張り出すために情報の整理を行います。
情報の整理の方法としては、主に ①図を描く ②グラフを描く ③別の条件に言い換える などがあります。
①図を描く
どんな問題でも図を描くようにしてみることが重要です。図にすることで、言葉だけでは読み取れない情報に気付くことができる可能性が上がります。
「問題は片っ端から図にしていく」この意識を持って問題に当たるようにしましょう。
悲しいことに、数学が苦手だという人ほど、問題を読んだ時から思考停止して図を書かないことが多いです…残念ながら、それでは数学は永遠に解けるようにはなりません。
②グラフを描く
これは関数の問題に多いのですが、必ずグラフを描くようにしましょう。
問題文の条件に合うようにグラフを描き、情報を書き込んでいくと、立式すべき条件が見えてきたり、具体的なイメージが湧きます。
関数は入試頻出分野です。この単元が得意になると、合格にグッと近づくのは間違いないです。
関数分野を得意にする第一歩が『グラフを描く』ことでしょう。
③別の条件に言い換える
①と②は想像がつくと思いますが、『別の条件に言い換える』というのは少し理解するのが難しいかもしれません。
要するに、立式がしやすいように問題文の条件(の中身)を変えずに日本語の表現を変えるということです。
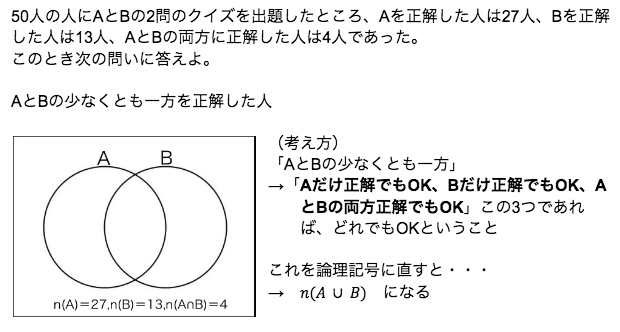
簡単な問題で例を挙げたいと思います。次の問題を見て下さい。
簡単な問題ですが、『翻訳』『情報の整理』『別の条件に言い換える』が全て登場する問題です。
他にもInstagramの方で大阪大学の問題を用いて解説を投稿していますので、ぜひご覧ください。
『式を立てる』→『計算』⇄『別の条件に言い換える』

立式さえ済めば後は計算していくだけです。
簡単な問題であればそれだけで答えに辿り着けるでしょう。
しかし、難しい問題の場合はそう上手くいきません。
計算していった結果、数式を見てまた別の条件に言い換えたり、図やグラフを描いて、また新しい式を立てる。そしてまた計算をして… という感じでループして最終的に答えに辿り着きます。
この流れは言葉で説明するのは非常に難しいです。
なので、皆さんが問題集を解くときに「今自分がどこの段階にいるのか」ということを意識して、自分で感じ取ってみて欲しいです。
そういう意識を持って問題を演習していると、結局やっていることは同じだな、と思えるようになると思います。その状態まで持っていけると数学のレベルは相当高くなっていると思います!
まとめ
今回は、数学の問題を解くときの思考過程について記事にしてみましたがいかがだったでしょうか。
毎度毎度のことで恐縮ですが、内容が抽象的で理解しづらかったかもしれません。
しかし、冒頭の画像の項目を意識して自分で問題を演習していくと、「あぁ、こういうことが言いたかったのか!」と理解してもらえると思っています。
数学なんてできないよ、と諦めてしまっては永遠に出来るようにはなりません。
ますは分からなくてもとにかく手を動かして何か書いてみることから始めてみましょう!
見ているだけで問題が解けるようになることは絶対にあり得ません。まずはそこからです。
今回は主に演習部分に重きを置いた記事になりましたが、次回の記事は『そもそも数学ってどうやって勉強していくんだ?』という方向けに記事を書きたいと思います。お楽しみに!








コメント